Mean field game (MFG) theory studies the strategies of agents of a large population in a competitive environment. Each agent seeks to maximise its own benefit according to the actions of other agents surrounded. For example, in the stock market, each trader buys or sells a certain number of shares based on other traders’ strategies in order to maximise his / her rates of return. The term "mean field" comes from physics, which means that the behaviour of an individual agent in a large population has negligible impact upon the system. In a typical MFG, an agent behaves based on the distribution of the states of other agents instead of reacting upon the behaviour of other agents individually. For instance, in a shopping market, a customer can buy some good after knowing the trading information of other customers and sellers, which is somehow impossible and troublesome. Instead, in a mean field scenario, he / she can decide based only on the price of the good, which simplifies the decision. In the market, the price is formed through the interaction of buyers and sellers. Thus, it encodes the probabilistic distributions of the states and strategies of all the agents in the market. The price, viewed as a mean field, enormously saves the time of making decisions.
The theory of MFGs is introduced in the mathematical field by J M LASRY and P L LIONS [1, 2], and is developed independently in the engineering community by P E CAINES, M HUANG and R P MALHAMÉ [3, 4]. MFGs are the limits of N-player games when N goes to infinity. In continuous time, a typical MFG consists of a Hamilton-Jacobi-Bellman equation that describes the dynamics of the cost function of an individual agent and a Fokker-Planck equation that describes the evolution of the aggregate distribution of agents. Until now, there are many applications of MFGs in, for example, economics [5, 6], social networks [7, 8], machine learning [9, 10] and so on.
In this article, we discuss several applications of MFGs, including interactions with machine learning, pedestrian flows, pandemic models, and MFGs for marriage.
1. MFGs and Machine Learning
The interactions between MFGs and machine learning fall into two directions. On one hand, machine learning serves an efficient tool to solve high dimensional MFGs, see [11, 12, 13] and see [14] for a review on numerical methods for MFGs. On the other hand, MFG theory is used to provide insights into the explanation and development in machine learning [15]. Here, we introduce the application of MFGs on cluster analysis and reinforcement learning.
1.1 Cluster Analysis
Cluster analysis is a classical problem in machine learning. There, people concern about subdividing a group of data points into subgroups such that points within a same group are close to each other than they are to elements in other groups, see [20, 21]. In [18, 19], MFG models are developed for Cluster Analysis, which correspond to the continuous versions of the K-means algorithm [21] and the Expectation-Maximisation algorithm [22], respectively.
In [19], the authors use a finite mixture model, which is a convex combination of probability density functions, to describe the given data set. They treat each data point as an agent of one of the populations. Every population represents a component of the mixture model. Each agent of some population moves according to its own dynamic and seeks to minimise an infinite horizon cost functional, which encodes the distance between the agent’s position and the population’s barycenter. Thus, they obtain a multi-population MFG system. One of the applications in [19] deals with the colour quantisation problem. The aim is to reduce the total number of colours in a given image to a fixed number K, in a way such that the resulting image is as similar as possible to the original one. Fig 1 shows the original gray picture and the colours’ distribution. Fig 2 reports the results for K = 2, 3, 5 clusters respectively. We see that as the number of clusters increases, the result picture gets closer and closer to the original image.
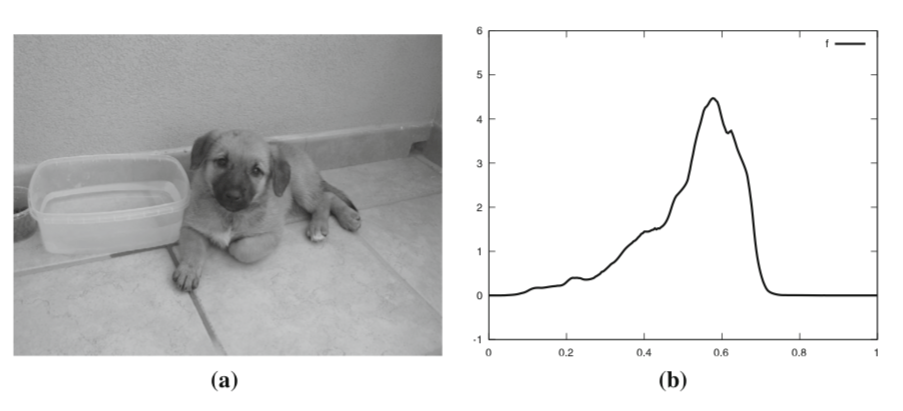
Fig 1. A black and white image (a) and its grey scales distribution (b) (Source: [19])
1.2 Multi-agent Reinforcement Learning (MARL)
Nowadays, reinforcement learning (RL) is one of the most popular research areas in deep learning. Typically, many famous applications of RL like AlphaGo are based on a single agent or agents of a small population. Agents make decisions based on the environment and receive rewards. MARL arises in more complex scenarios. For example, in traffic networks, the action of a driver is influenced by the environment and other drivers surrounded. Thus, in traffic flows, we need to take into account the behaviour of a large number of agents. Recently, MARL has succeeded in some applications.
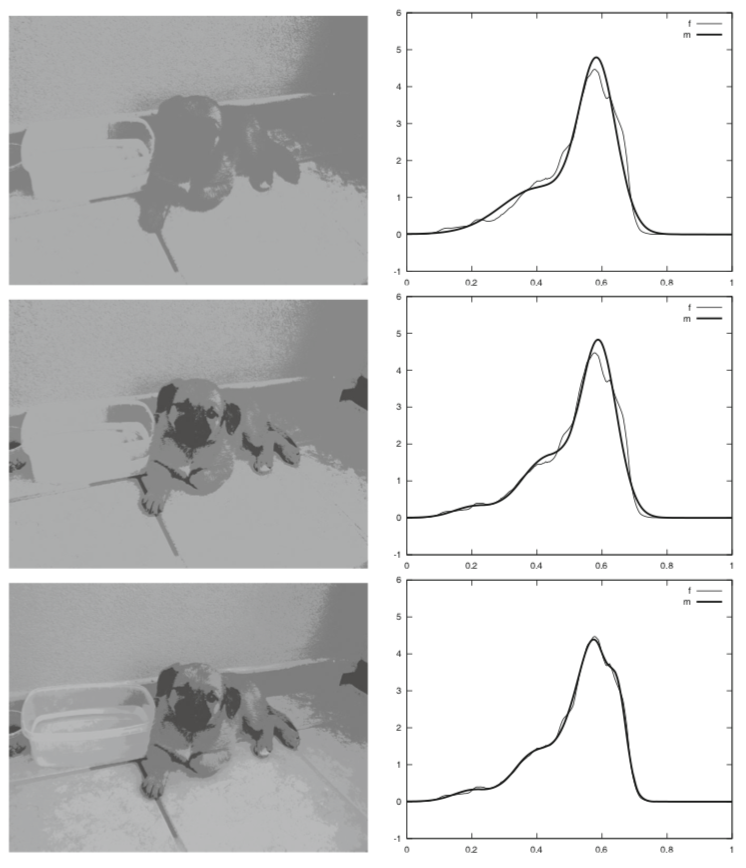
Fig 2. Colour quantisation via MFG clustering (left panels) and the corresponding mixtures (right panels), for K = 2, 3, 5 (from top to bottom panels) (Source: [19])
For instance, OpenAI builded a system that can beat Dota2 and DeepMind did the same on the Quake III game. Generally, MARL is harder to deal with when the number of agents increases due to the computational complexity of directly solving Nash equilibrium. The MFG approach can be used to simplify the complexity of MARL scenarios with a large number of agents. Instead of reacting upon the actions of other agents individually, each agent performs with respect to the distribution of other agents, which represents the collection of actions and states of other agents.
In [16, 17], the authors propose different techniques of combining MFG and MARL. One of the experiments in [16, 17] deals with mixed cooperative-competitive battle game. In the game, two armies fight against each other in a grid world, each of which is empowered by a different RL algorithm. In the setting of Fig 3a, each army contains 64 homogeneous agents. Each army can get more rewards by collaborating with teammates to destroy all the components. In the example, the algorithms, Q-learning (QL) and advantageous actor (AC), are tested against their mean field counterparts, mean field Q-learning (MF-Q) and mean field advantageous actor (MF-AC). They train all four models by 2000 rounds self-plays. During the training, agents quickly pick up the skills of chasing and cooperation to kill the opponents. Fig 4 shows the result of winning rate and the total reward over 2000 rounds cross-comparative experiments. We see that MF-Q largely outperforms other algorithms, which shows the effectiveness of the mean field MARL algorithm.
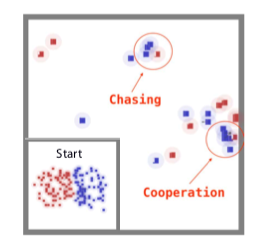
(a) Battle game scene
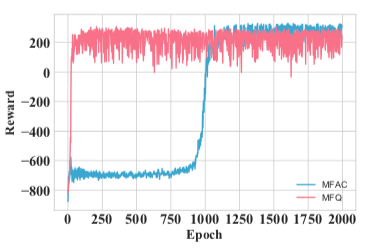
(b) Learning Curve
Fig 3. The battle game: 64 vs 64 (Source: [16])
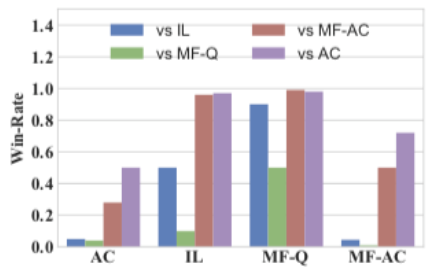
(a) Average wining rate
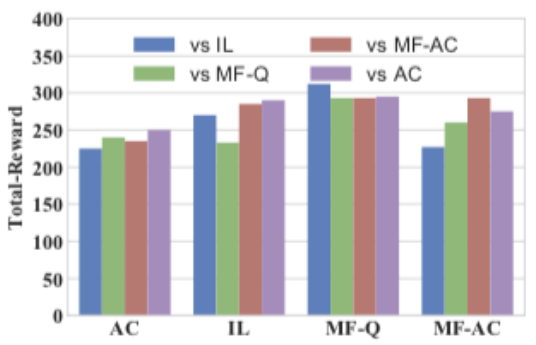
(b) Average total reward
Fig 4. Performance comparisons in the battle game (Source: [16])
There are still other interesting applications of MFGs in learning that we do not introduce here. For example, [24] presents a general MFG framework for simultaneous learning and decision-making and does experiments on repeated Ad auction problems. Combining MFGs and machine learning is still purely theoretical and has not been widely used in the industry. However, the initial attempts show an incredible potential. MFGs can provide a rigorous framework towards learning tasks and simplify the complexity for the system involving a large scale with infinite agents.
2. Pedestrian Flows
The flows of pedestrians consist of decisions of a large number of agents. Typically, in pedestrian flows, we always need to consider congestion effects, where the cost of a single agent depends on the nonlinear combination of the velocity of movements of agents and the distribution of the whole population, in a way such that, for example, in a very crowded area, agents prefer to move slowly. MFGs with congestion effects was introduced and studied by P L LIONS in [25] in 2011, see also [14, 26, 27, 28] for some numerical simulations.
Here, we introduce the example from [14, 28]. In [14, 28], the authors model a situation where pedestrians are driven to leave a given square hall with rectangular obstacles, which is shown in Fig 5.
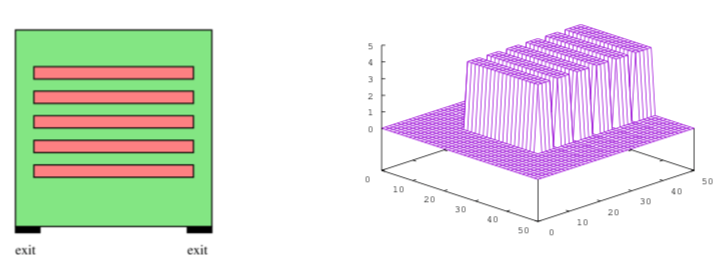
Fig 5: Left: the geometry (obstacles are in red); Right: the density at t=0 (Source [14])
In Fig 5, the hall has obstacles marked red and two exits at the bottom. One can imagine that there is a panic in the closed building, where pedestrians try to reach the exit doors, and that the obstacles marked red are chairs. At t=0, all the people are sitting in the chairs, as shown at the right-hand side of Fig 5. Fig 6 shows the probability density of people at t=1, 5 and 15 minutes. We see that pedestrians rush towards the closest narrow corridors at the left and right sides of the hall and then run to the exits. We also notice that the population density reaches high values at the intersections of corridors. In the work [14, 28], the authors also notice the congestion effects, that is, the velocity is low in the regions where the density is high.
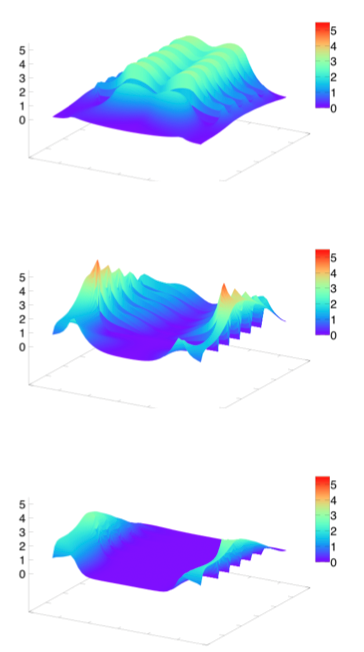
Fig 6. The density computed with the two models at different dates, t = 1, 5 and 15 minutes (from top to bottom) (Source [14])
3. Pandemic Models
The coronavirus disease 2019 (COVID-19) pandemic is shaping our world on a global scale. There are a bunch of research papers concerning about the COVID-19 models. The MFG theory is an efficient tool to study the pandemic involving the actions of people in a large population. Several papers provide different MFG models for COVID-19, see [29, 30, 31]. In [29], the authors give a mean field control model in controlling the propagation of epidemics on a spatial domain. The model in [29] is based on the well-known SIR model [32], where S, I, and R represent the number of susceptible, infected and recovered people, respectively. The classical SIR model consists only ordinary differential systems concerning the evolution in time. Since serious pandemics like COVID-19 propagate throughout the world, it is essential to consider spatial-like SIR models to consider the spread of the disease and the infection and movement of people. In [29], the authors combine ideas from the SIR model and MFG to model the spread of the virus in a spatial domain. The goal of the model is to minimise the number of agents infected and the amount of movement of the population.
One of the experiments in [29] studies the influence of different recover rates.
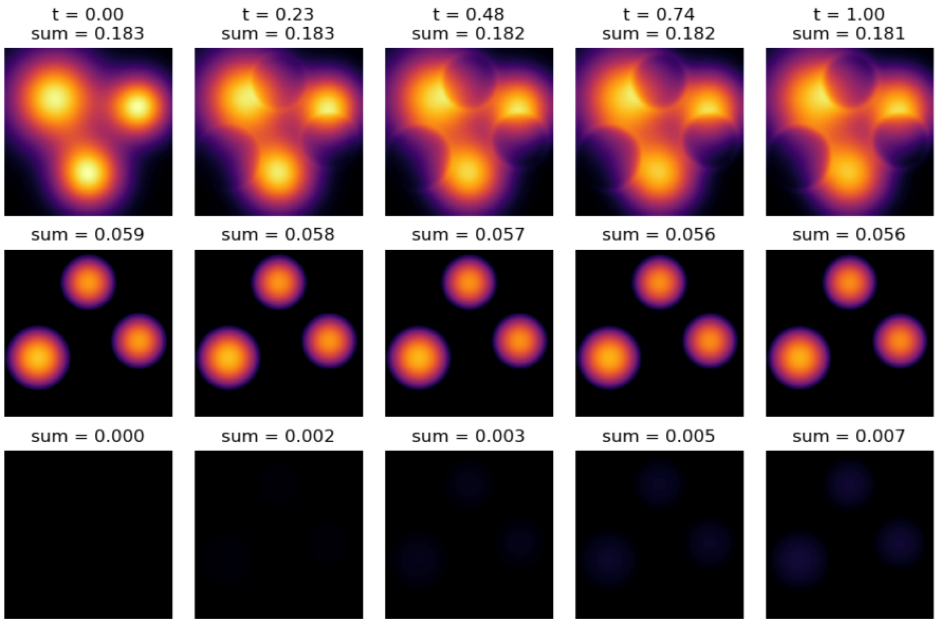
Fig 7. The evolution of populations for different time with a lower recovery rate. The first row represents susceptible, the second row represents infected, and the last row represents recovered. (Source: [29])
Fig 7 shows the probability densities of populations from t=0 to t=1 for a low recover rate. The first row of Fig 7 represents the evolution of the susceptible, the second row shows the movement of the infected people, and the last row depicts the changes of the recovered population. As time evolves, we see that the susceptible population is separated from the infected people. This suggests that when the recovery rate is low, the optimal strategy is to prevent susceptible population from becoming infected.
Fig 8 plots the evolution of the populations when the recovery rate is high, which happens when the vaccine comes to the public. In Fig 8, the susceptible population does not move that much over time. There are less people getting affected and more people recovered. This experiment implies that when the recovery rate is high, the optimal strategy is to focus on recovering the infected people rather than moving the susceptible population, in order to reduce the number of infected.
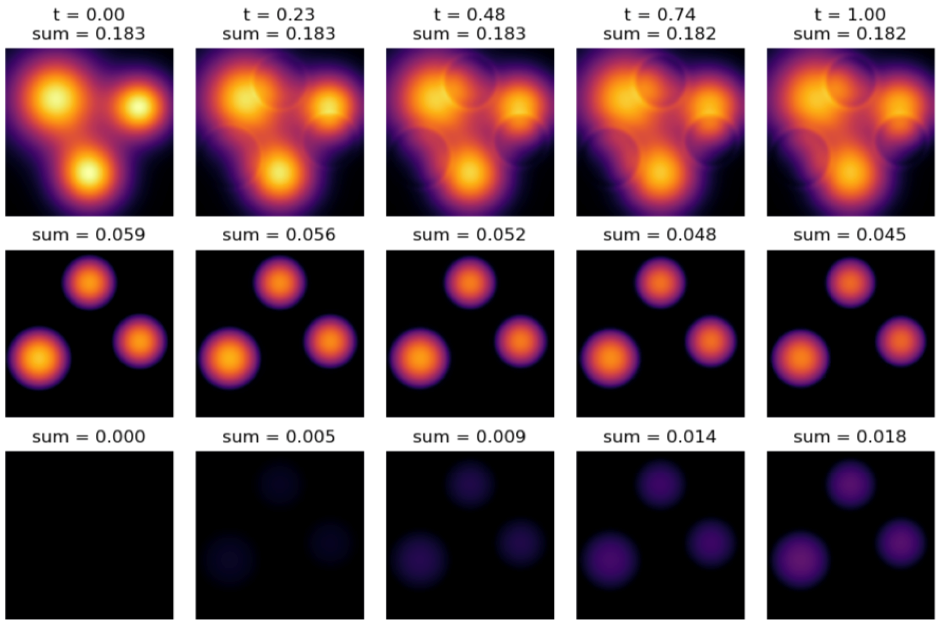
Fig 8. The evolution of populations for different time with a high recovery rate. The first row represents susceptible, the second row represents infected, and the last row represents recovered. (Source: [29])
4. MFGs for Marriage
As the last example, we introduce an interesting application of MFGs for marriage. In [33], the authors use stochastic differential equations to model the feeling state of a couple. The feeling state is influenced by random events, parents, children, friends, and the social distribution of marital status. Mathematical models can help us to have more understanding on the sentimental dynamics and to propose a suitable intervention or therapy for a couple. The works before [33] do not consider the influence of uncertainty, noise, random events, and the social distribution of feeling states. A mean field model is a desired model for such problem since the society, friends, and parents of a couple may join together to influence them. The mean field term in the model of [33] refers to the distribution of couple feeling states in the society.
In [33], the authors consider a mean field sentimental game. They get a consensus that the felling states of friends, parents, friends of friends and social environment can also have impact on a couple. For instance, a couple has a high chance to divorce if many of the friends are in lower feeling states. Moreover, a couple’s feeling state will also propagate and influences their friends’ friends and so on. Therefore, the authors introduce society’s social influences and external impact into the marital game.
In the numerical results, the study in [33] suggests that the effort of a couple to refresh their marriage may help in sustaining marriage if the cost of the effort is not too high and the initial feeling state is not too low. It also shows that knowing too many divorced people may have a counter-productive influence on the status of a marriage. The more divorced people you know, the high possibility that your own marriage will break down. But it does not mean that a couple will divorce just because their friends’ marriages are breaking down. Marital status also depends on the efforts of couples and the social environment. This study helps us understand theoretically the processes related to marriage, which can be useful to design or evaluate an intervention towards a marriage.
The applications discussed above are far from complete. Indeed, as we can see from the aforementioned examples, the MFG theory offers an efficient tool to model systems involving a large number of agents. It is very promising to see more and more interactions of MFGs and other fields in the current “Big Data” trend.
References
- J. M. Lasry and P. L. Lions, Jeux à champ moyen. I. Le cas stationnaire. C. R. Math. Acad. Sci. Paris, 343(9):619–625, 2006.
- J. M. Lasry and P. L. Lions, Jeux à champ moyen. II. Horizon fini et contrôle optimal. C. R. Math. Acad. Sci. Paris, 343(10):679–684, 2006.
- M. Huang, P. E. Caines, and R. P. Malhamé. Large-population cost-coupled LQG problems with nonuniform agents: individual-mass behavior and decentralized ϵ-Nash equilibria. IEEE Trans. Automat. Control, 52(9):1560–1571, 2007.
- M. Huang, R. P. Malhamé, and P. E. Caines. Large population stochastic dynamic games: closed-loop McKean-Vlasov systems and the Nash certainty equivalence principle. Commun. Inf. Syst., 6(3):221–251, 2006.
- Y. Achdou, J. Han, J. M. Lasry, P. L. Lions, and B. Moll. Income and wealth distribution in macroeconomics: A continuous-time approach. Technical report, National Bureau of Economic Research, 2017.
- G. Olivier, J. M. Lasry, and P. L. Lions. Mean field games and applications. In Paris-Princeton lectures on mathematical finance 2010, pp. 205-266. Springer, Berlin, Heidelberg, 2011.
- B. Dario, H. Tembine, and T. Basar. Opinion dynamics in social networks through mean-field games. SIAM Journal on Control and Optimization 54, no. 6 (2016).
- L. Jian, B. Xia, X. Geng, H. Ming, S. Shakkottai, V. Subramanian, and L. Xie. Mean field games in nudge systems for societal networks. ACM Transactions on Modeling and Performance Evaluation of Computing Systems (TOMPECS) 3, no. 4, 2018.
- C. Haoyang, X. Guo, and M. Laurière. Connecting GANs, MFGs, and OT. arXiv e-prints (2020): arXiv-2002.
- S. Jayakumar, and A. Mahajan. Reinforcement learning in stationary mean-field games. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, pp. 251-259. 2019.
- C. René, and M. Laurière. Convergence Analysis of Machine Learning Algorithms for the Numerical Solution of Mean Field Control and Games: II--The Finite Horizon Case. arXiv preprint arXiv:1908.01613 (2019).
- C. René, and M. Laurière. Convergence Analysis of Machine Learning Algorithms for the Numerical Solution of Mean Field Control and Games: II--The Finite Horizon Case. arXiv preprint arXiv:1908.01613 (2019).
- R. Lars, S. J. Osher, W. Li, L. Nurbekyan, and S. W. Fung. A machine learning framework for solving high-dimensional mean field game and mean field control problems. Proceedings of the National Academy of Sciences 117, no. 17, 2020.
- A. Yves, and M. Laurière. Mean field games and applications: Numerical aspects. arXiv preprint arXiv:2003.04444, 2020.
- W. E, J. Han, and Q. Li. A mean-field optimal control formulation of deep learning. Research in the Mathematical Sciences 6, no. 1 (2019): 1-41.
- Y. Yang, R. Luo, M. Li, M. Zhou, W. Zhang, and J. Wang. Mean field multi-agent reinforcement learning. In International Conference on Machine Learning, pp. 5571-5580. PMLR, 2018.
- M. David, J. Jennings, S. V. Macua, E. Sison, S. Ceppi, and E. M. D. Cote. Coordinating the crowd: Inducing desirable equilibria in non-cooperative systems. arXiv preprint arXiv:1901.10923, 2019.
- J. L. Coron. Quelques exemples de jeux à champ moyen, Ph.D. thesis, Universite Paris-Dauphiné, 2018.
- A. Laura, S. Cacace, F. Camilli, and R. D. Maio. A mean field games approach to cluster analysis. Applied Mathematics & Optimization (2020): 1-25.
- B. Christopher M. Pattern recognition and machine learning. springer, 2006.
- S. Amit, M. Prasad, A. Gupta, N. Bharill, O. P. Patel, A. Tiwari, M. J. Er, W. Ding, and C. Lin. A review of clustering techniques and developments. Neurocomputing 267 (2017): 664-681.
- B. Leon, and Y. Bengio. Convergence properties of the k-means algorithms. In Advances in neural information processing systems, pp. 585-592. 1995.
- J. A. Bilmes. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. International Computer Science Institute 4, no. 510 (1998): 126.
- X. Guo, A. Hu, R. Xu, and J. Zhang. Learning mean-field games. arXiv preprint arXiv:1901.09585 (2019).
- P. L. Lions, Cours du Collège de France, http://www.College-de-france.fr/default/EN/all/equ−der/, 2007-2011.
- Y. Achdou. Finite difference methods for mean field games. In Hamilton-Jacobi equations: approximations, numerical analysis and applications, pp. 1-47. Springer, Berlin, Heidelberg, 2013.
- Y. Achdou, and J. M. Lasry. Mean field games for modeling crowd motion. In Contributions to partial differential equations and applications, pp. 17-42. Springer, Cham, 2019.
- Y. Achdou, and M. Lauriere. On the system of partial differential equations arising in mean field type control. arXiv preprint arXiv:1503.05044 (2015).
- W. Lee, S. Liu, H. Tembine, W. Li, and S. Osher. Controlling Propagation of epidemics via mean-field control. SIAM Journal on Applied Mathematics 81, no. 1 (2021): 190-207.
- S. Cho. Mean-field game analysis of SIR model with social distancing. arXiv preprint arXiv:2005.06758 (2020).
- A. Alexander, R. Carmona, G. Dayanikli, and M. Lauriere. Optimal incentives to mitigate epidemics: a Stackelberg mean field game approach. arXiv preprint arXiv:2011.03105 (2020).
- W. O. Kermack, and M. G. Anderson G. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character115, no. 772 (1927): 700-721.
- B. Dario, B. M. Dia, B. Djehiche, H. Tembine, and R. Tempone. Mean-field games for marriage. PloS one 9, no. 5 (2014): e94933.
Author:
Dr MOU Chenchen, Assistant Professor, Department of Mathematics, City University of Hong Kong
July 2021

