(1) 引言
如果你拨动一条小提琴的琴弦,琴弦振动的同时,亦驱使它附近的空气粒子振动,形成声波在空气中传播,这就是为什么你可以听到琴音。不过,这乐音不会持久。在发出声波的同时,琴弦会损失它振动的能量。所以,琴弦的振动会衰减,琴音亦然。
有趣的是,受扰动的黑洞都有类似的现象。当两个黑洞相撞后,它们会合并成一个更大但被扭曲了的黑洞,同时产生重力波。这个被扭曲了的黑洞就是受扰动的黑洞的一个例子。重力波其实就是新形成的黑洞周围时空的振荡。跟小提琴琴弦相似的是,这些时空的振荡不会持久,因为黑洞是一种具有事件视界的天体。事件视界像是黑洞的一个只可以单向行车的高速公路。任何物件,一旦进入了事件视界,就无法离开。所以在黑洞附近传播的重力波,要不就是耗散到黑洞的事件视界,要不就是传播到离黑洞很远的地方,远至我们都可以探测到。无论如何,在黑洞附近的重力波总是在散失它的能量,黑洞的振荡亦然。当这些振荡减到很弱时,被扭曲了的黑洞就会变成一个很安静的静态黑洞。由于黑洞振荡的衰减过程类似于乐器(例如一个响铃)发出的乐音的衰减,黑洞振荡的衰减亦都叫做「铃荡」。就像一条琴弦都有不同的振荡模态(基音和泛音),黑洞振荡都有不同的振荡模态。这些振荡模态命名为黑洞的准简正模(quasinormal modes),相关的振动频率则称为准简正模频率(quasinormal-mode frequency)。
黑洞铃荡不单纯是理论物理的一个研究课题,这是一个实在的天文物理现象,打从我们由先进激光干涉仪重力波观测站(the Advanced Laser Interferometer Gravitational-Wave Observatory, aLIGO)第一次直接量度到重力波时,我们就已经观察到黑洞铃荡。首次直接探测到的重力波讯号(GW150914)的末段,就清楚显出一个由相重力波波源所形成的新黑洞所发出的铃荡讯号。自此,天体物理学家就广泛地研究重力波讯号中的铃荡讯号。
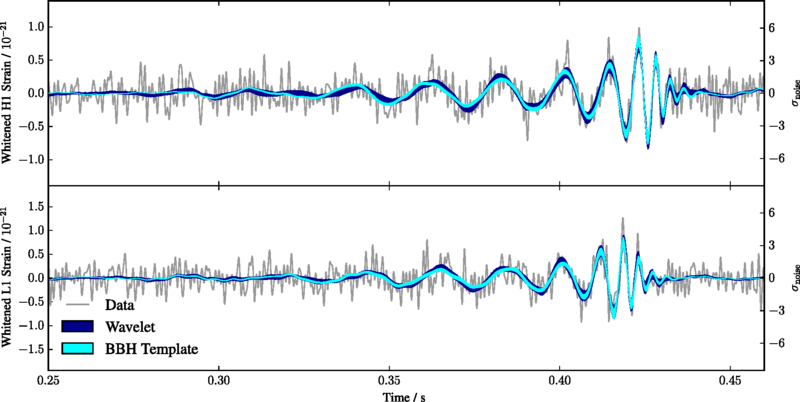
图1: 先进激光干涉仪重力波观测站第一次直接量度到重力波时的重力波讯号。在讯号的末段,我们可见一个黑洞振动的衰减。图片取自[1]。
(2) 为什么要关心黑洞铃荡?
但为什么天体物理学家很热衷于研究黑洞铃荡?笔者认为有两大理由。
首先,铃荡讯号是一个独特而有效的探究工具,让我们去研究基础物理中未能解答的问题,例如爱因斯坦的广义相对论在强重力的时空中—例如事件视界附近—是否还是正确的?相对论是一个斐然的理论,把重力作用演绎为时空的几何效应,它亦代表了我们对时空的最佳解读。但是,广义相对论亦有些地方不能提供令人满意的解释,例如重力的量子本质。这些都反映广义相对论有其局限,需要增补。但从何著手?为了揭示广义相对论需要修补的地方,科学家进行了大量实验,务求检验广义相对论。不过可能令到某些物理学家失望的是,广义相对论暂时都通过了所有的测试!但是,大部份这些测试都只涉及较弱的重力场,因为此前的测试,大都是在地球上或者是太阳系或星系内进行的。广义相对论通过了这些全部的测试,反映广义相对论要是失效的话,它只可以在重力非常强的时空—例如事件视界周围—崩溃。要是广义相对论真的不能正确描述强重力时空和黑洞振荡的动态的话,那我们将会观察到跟广义相对论预测不同的黑洞振荡模式。换言之,分析铃荡讯号是测试广义相对论在强重力时空中表现的理想工具。
第二,在研究黑洞振动的同时,我们会发展出多种数学工具。这些数学工具,都可以推动不同范畴的科研。为了正确了解铃荡讯号,我们必须预先理解黑洞振动的模式。数学上,黑洞振荡由一组偏微分方程(partial differential equations)所描述。所谓偏微分方程,其实是偏导数(partial derivatives)所需要满足的数学关系。而偏导数描述的是一个量怎样随住几个不同的有关变量而改变[2,3]。研究黑洞扰动时,这些偏微分方程刻画了黑洞的振幅怎样随住时间和位置而改变。除了黑洞物理外,偏微分方程在其他科研范畴都有广泛应用。与日常生活有关的例子包括股票市场、天气预报、电话通讯、光纤网络和生物物理。通常偏微分方程都是很难解的,而描述黑洞振动的方程亦无例外。要克服这些数学挑战,包括笔者在内的黑洞物理学家,致力发展新颖的数学技巧去解开这些复杂的方程式。这些数学技巧,亦可以用于解开出现于其他研究范畴的偏微分方程。
(3) 我们可以学到什么?
正如一位专业小提琴演奏家听到一个琴音,就可以立即辨别出琴音的音调、琴弦的粗幼和琴马的状态;一位钻研黑洞的物理学家亦可透过仔细分析铃荡讯号中,就可以推敲出黑洞的各样特性。如图一所示,一个铃荡讯号是衰减的振荡。物理学上,一个衰减的振动可以用两个数字去描述:频率—振动的快慢和衰减期—振动消减的率。根据广义相对论,黑洞的质量和转动速率就完全决定了所有振动模式的频率和衰减期。一个质量较大的黑洞振动频率较慢;一个转动得更快的黑洞,我们通常可以观察到的振动模态就会更持久。故此,透过量度铃荡讯号中的振动频率和衰减期,我们可以计算出黑洞的质量和转动速率。除此之外,我们更可以透过比对量度的和广义相对论预测的振动频率和衰减期,去检视广义相对论是否正确描述了黑洞事件视界附近的动力学。综合所有迄今已观察到的铃荡讯号,物理学家尚未观察到黑洞违反广义相对论的迹象。可能令人失望亦可能令人心安,广义相对论又再通过了一次测试。不过我们毋须过度失望,亦不能安于现况,因为这些结果归根究底还是受到探测器的敏感度所限。换言之,我们仅是在观察仪器的敏感度所容许的范围内没有观察到广义相对论失效的迹象。而先进激光干涉仪重力波观测站和处女座重力波团队探测器刚刚已再重新启动,它将会以前所未有的敏感度去侦测重力波讯号。我们会否观察到广义相对论失效的迹象呢?且让我们拭目以待。
(4) 我们如向从中学习?
但要正确和充分明白这些测试广义相对论的结果,我们必先了解黑洞要是违反广义相对论的话,会发出怎样的铃荡讯号。否则,即使我们真的侦测到广义相对论失效的迹象,我们都可能会误当这些迹象是另一个正常黑洞的铃荡讯号,只是质量和转动速率有所不同。为此,我们要广泛地研究种种广义相对论失效时黑洞铃荡的讯号。
如上所述,要研究黑洞振动,我们要解开一组冗长的偏微分方程。要考虑到黑洞的自转的话,方程式就更长了。但另一方面,由于已观察到的黑洞中,有些自转得很快,我们不可以忽略黑洞自转。考虑到自转后,这些偏微分方程确切有多繁复?如果你想把当中最短的一条方程打印到A4纸上,你需要56页!而你不单要解开一条,你起码要同时解开至少六条更长的方程式。对于广义相对论所描述的黑洞,我们尚且可以根据它们独有的几何性质来利用一些高明的数学技巧以简化这些冗长的方程式至一条。但是对于违反广义相对论的自转黑洞,我们不能重施故技,因为这些黑洞没有相同的几何性质。故此,我们现有的大部分方法,都只够我们用来研究转动得很慢的黑洞在不遵守广义相对论时的振荡情形。在没有了解到自转黑洞在违反广义相对论时的铃荡,我们无法利用已经探测了的铃荡讯号去透切地测试广义相对论。
为了解决这个问题,笔者在伊利诺大学厄巴纳-香槟分校跟尼古拉斯.苑尼斯教授和柏迪.华格里博士合作,正在发展一套方法在不需化解方程的情况下,直接解出这些冗长的偏微分方程。由于在不同情况下振动的黑洞,相关的偏微分方程都有类似的数学结讲,要是我们可以直接解出这些偏微分方程而毋须化解的话,我们就可以直接把我们的方法,用在研究转动黑洞在不同情况下的振荡,包括广义相对论失效或者黑洞附近存在暗物质时的情形。
这套方法的关键在于我们把代表黑洞振幅的量预先表达成谱函数(spectral function)的线性组合。谱函数是一类非常独特的函数,因为它们可以用来很准确地拟近其他函数。而所谓的线性组合,就是把谱函数,适当乘上一个合适的权重(称为谱系数,spectral coefficient),再进行加减。这是一个很有用的性质,因为不是每一种函数都是基础函数,例如对数函数、指数函数,和满足各样微分方程的函数。这些数学函数的性质并不显而易见。另一边厢,物理学家都熟识谱函数,用它们时也很方便。利用谱函数来拟近其他函数通常都可以帮助物理计算。举例,如果我们想拟近图二中蓝线所代表的函数(涉及到指数函数),我们只需要6个谱函数就办到,而且准确的程度是拟近出来的函数(红线)和原本的函数在图2中根本看不出任何分别。
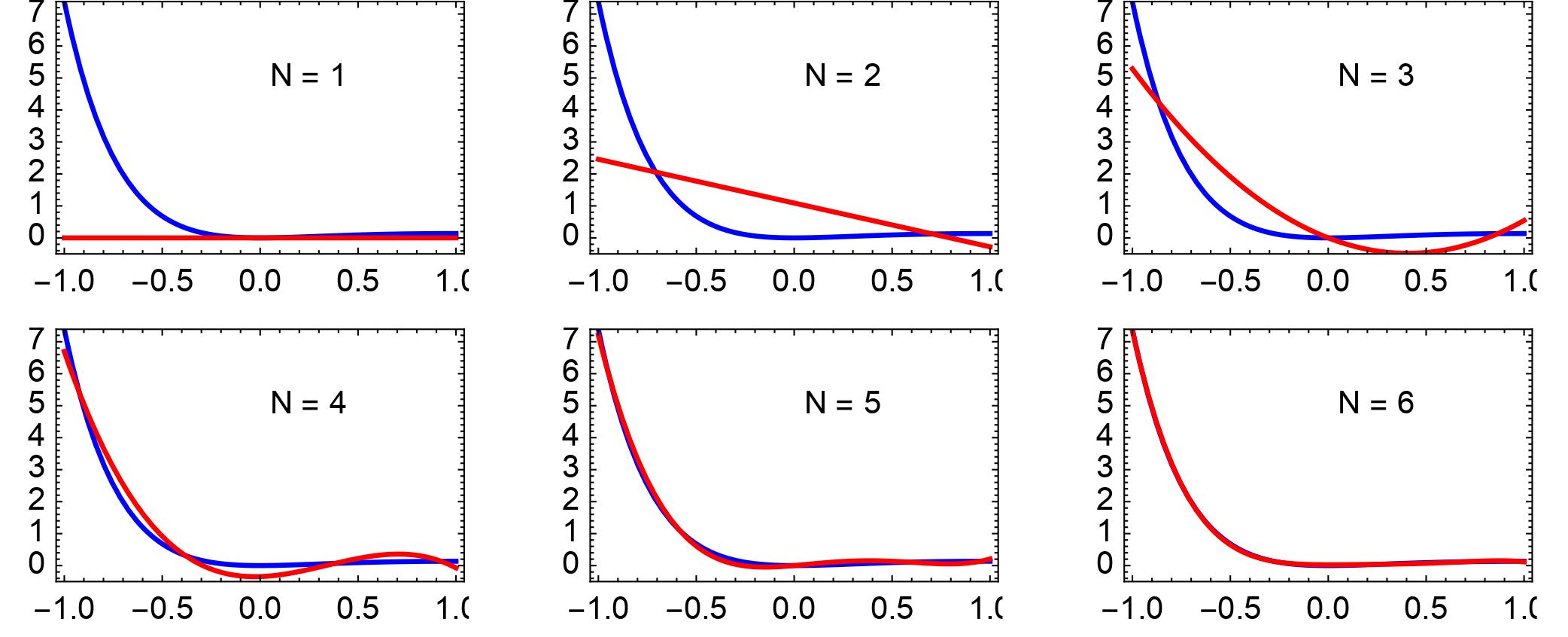
图2: 谱函数一个有趣的性质是它们可以用来拟近其他函数。例如如有我的想拟近图中蓝色线所代表的函数,我们只需要用6个谱函数就可以很准确地拟近,致使我们的拟近和原本的函数视觉上几乎没有分别。图片取自[4]。
谱函数的这特性在求解偏微分方程时就大派用场。如果我们先把满足方程的未知函数写成谱函数的线性组合,那原先的偏微分方程就会变成谱系数的代数方程。一般而言,代数方程都比微分方程易解得多。作为发展这方法的第一步,我们先把这方法运用在不自转但又遵守广义相对论的黑洞,看看我们可否用这方法计算出这简单黑洞已知的振动频率[5]。结果就如图三所示,运用谱方法我们可以极准确地算出这黑洞的振动频率。图3中的蓝点是我们用谱方法计算出的频率,而黑色交叉就是已知的频率。只要我们用足够多的谱函数,我们就可以准确计算到黑洞的准简正模频率。
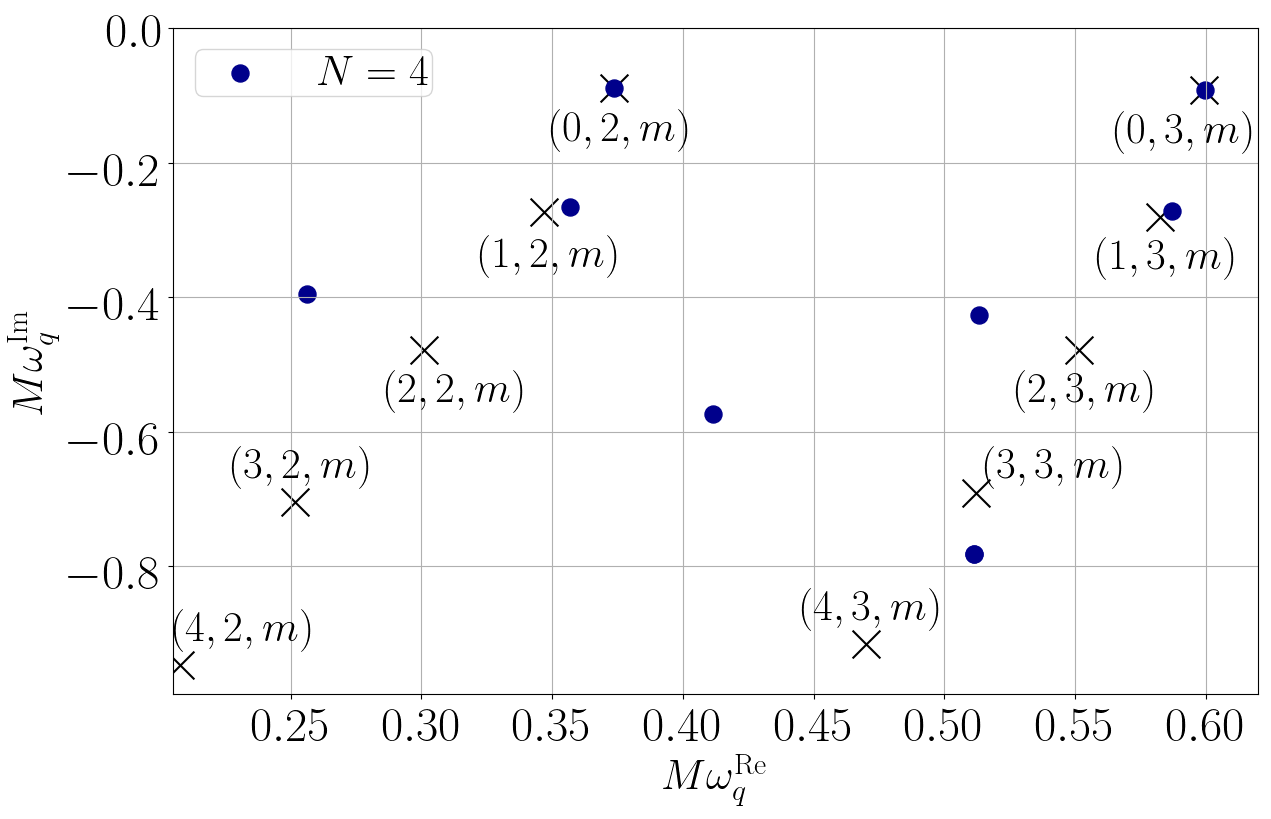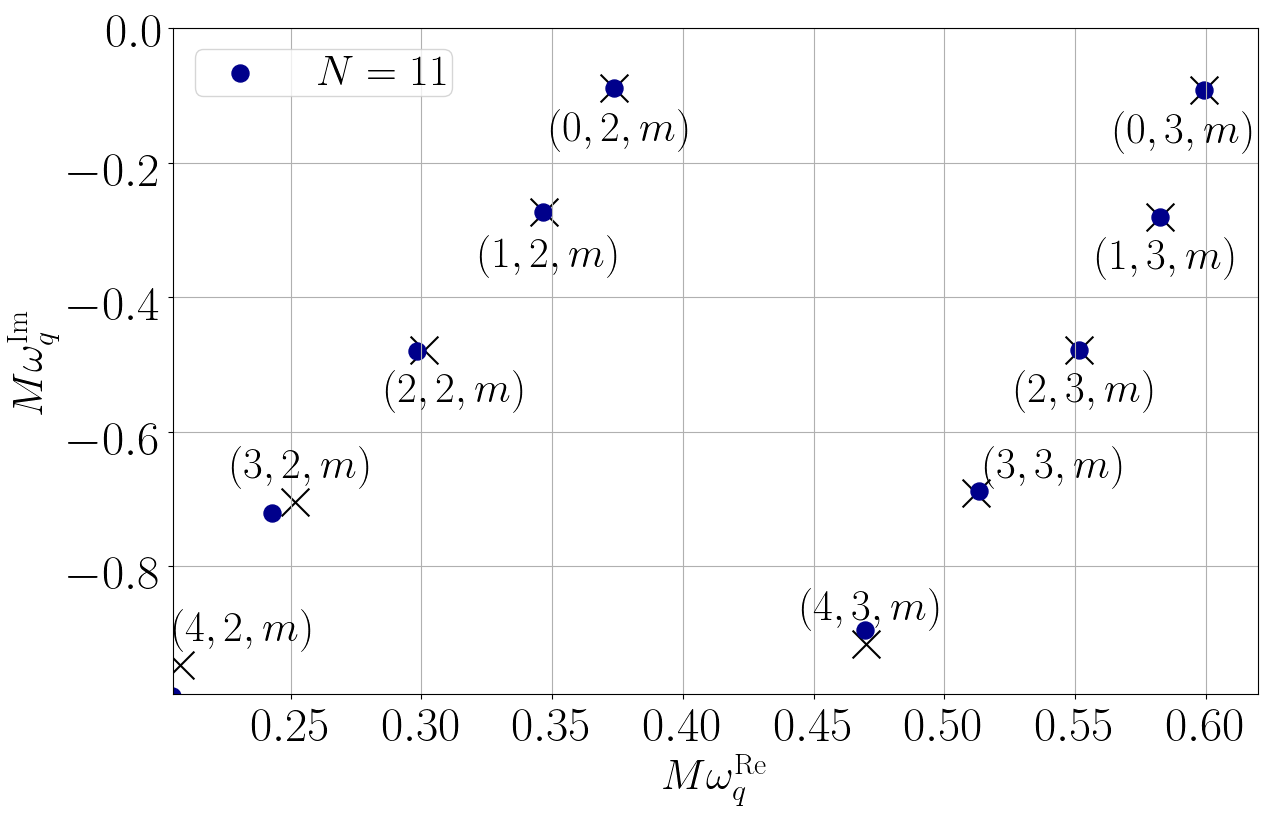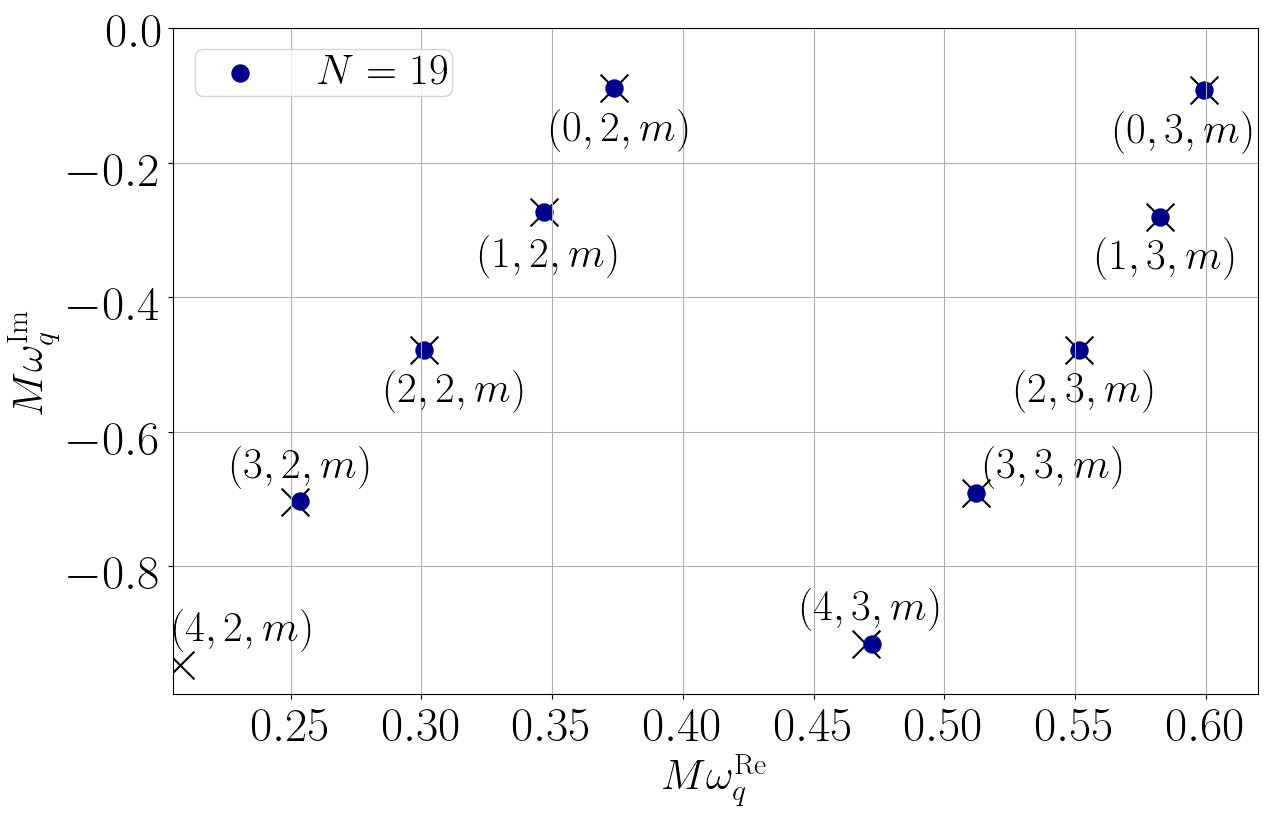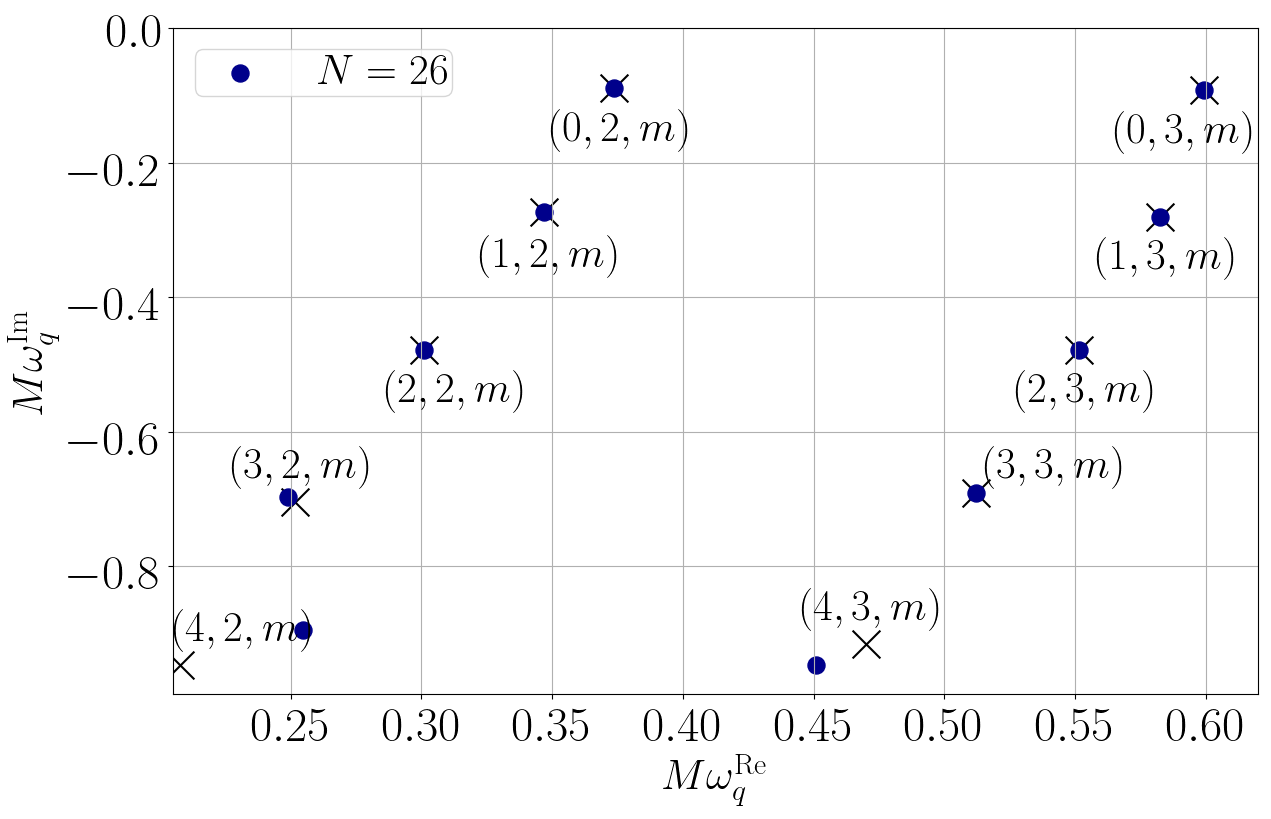
图3: 我们用我们的方法计算不自转但又遵守广义相对论的黑洞的振动频率(蓝点)。当我们用上愈来愈多的谱函数(数目由N表示),我们的结果就跟已知的频率(黑色交叉)愈趋吻合。图片修改自[5]。
我们现正致力继续发展这方法,令它可以用到广义相对论中的转动黑洞上。如果我们亦可以准备地算出这类黑洞的振动频率,我们就可以确认我们的方法准确无误,而且可以运用到其他用现有方法无法研究的黑洞上。在往年由香港桂冠论坛主办的智者.智讲青年科学家焦点小组(天文学)上,我已经展示过这方法在转动黑洞上的初步结果[6]。我们现正准备相关的论文,交代这个运用谱方法的详细步骤。
(5) 展望
计算出黑洞的准简正模频率只是第一步。得出不同黑洞的准简正模谱后,我们须用这个谱来对比我们观察到黑洞铃荡讯号,从而推敲广义相对论需要修正的方向和程度。这些计算和观察都能令我们更好的去聆听和了解黑洞振荡发出的乐音,从而去了解我们身处的宇宙。
延伸阅读
- 基普.索恩教授著《黑洞和时空扭曲》的第十章
- Pedro G. Ferreira教授著 《完美的理论:一整个世纪的天才与广义相对论之战》
- 丘成桐教授和史蒂夫.纳迪斯教授著《丘成桐谈空间的内在形状--几何、弦论和宇宙中隐藏起来的维度》第五章
鸣谢
笔者在此感谢程国平先生、卢乐知先生和尼古拉斯.苑尼斯教授对本文初稿的意见。
参考资料︰
- Properties of the Binary Black Hole Merger GW150914, B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. Lett. 116, 241102, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.241102
- 丘成桐教授和史蒂夫.纳迪斯教授著《丘成桐谈空间的内在形状--几何、弦论和宇宙中隐藏起来的维度》第五章有关于偏微分方程更详细的科普导引
- 读者要是中学时有学过微积分,可能会记得导数的概念。这导数叫做常导数(ordinary derivative),因为只涉及一个量怎样随另一个量改变。偏导数涉及的是一个量随几个量改变,故此偏导数可以视为常导数的延伸。
- A new approach and code for spinning black holes in modified gravity, by Pedro G. S. Fernandes, David J. Mulryne, https://arxiv.org/abs/2212.07293
- Spectral Method for the Gravitational Perturbations of Black Holes: Schwarzschild Background Case, Adrian Ka-Wai Chung, Pratik Wagle, Nicolas Yunes, accepted for publication by Physical Review D, https://arxiv.org/abs/2302.11624
- https://www.youtube.com/watch?v=MDeALFtz-Uc&list=PLkIh51n7eBb2Y5f559D4wTsY2L4GPH2hc&index=2&ab_channel=HongKongLaureateForum
作者︰
钟嘉唯先生
伊利诺大学厄巴纳-香槟分校物理系博士后研究员
伊利诺高等宇宙研究所成员
2023年10月

