极小曲面是微分几何学里最重要的研究对象之一。极小曲面除了本身富有数学美之外,在诸多物理现象中亦会自然出现,例如相变(phase transition)[1] 以及蝴蝶翅 膀鳞片的生物光子纳米结构[2](图1)。极小曲面在材料科学、工程学,甚至艺术、建筑领域均占有席位。 Frei Otto 亦在几项建筑作品的设计中运用了极小曲面,包括1972年德国慕尼黑奥林匹克运动场(图2)。

图1 - 蝴蝶翅膀鳞片中的螺旋二十四面体(gyroid)结构(资料来源:[2])

图2 -位于慕尼克北部的慕尼黑奥林匹克公园正中心的奥林匹克运动场,乃1972年夏季奥运会的主要会场(资料来源: https://munich-info.info/olympic_stadium_munich/)
肥皂膜及普拉托的实验 事实上,要窥探何谓极小曲面,并不需要有科学家或建筑师的知识水平,因为这类曲面其实我们自小就见过,就是肥皂膜以及其类似的形态 - 肥皂泡。如果将一条金属圈浸入皂液再取出,就会看到线的边缘拉出一层薄肥皂膜。例如,用圆形线圈可以拉 出一只平碟。如果用两个平行同轴圆形线圈,就会拉出一个旋转对称肥皂膜,这种型状叫作悬链曲面(catenoid)(图4)。在十九世纪 ,比利时物理学家兼数学家约瑟夫.普拉托(Joseph Plateau)是首位利用不同形状金属线做实验、大规模研究肥皂膜的学者。他从实验的观察结果总结出一套名为「普拉托定律」的法则,用以描述一切有可能形成的肥皂膜之形状及特性(图5)。

图3 - 平碟形(左)及悬链曲面(右)肥皂膜(资料来源:http://soft-matter.seas.harvard.edu/index.php/Soap_films)

图4 - 肥皂膜所呈现的普拉托定律 (资料来源:“The Geometry of Soap Films and Soap Bubbles”《肥皂膜及肥皂泡的几何学》, F Almgren and J Taylor, Scientific American (1976))
肥皂膜所蕴含的数学 普拉托的实验灵感源自Joseph-Louis Lagrange于1760年提出的一个数学问题——给定固定边界后,是否总是存在面积达至最小的曲面?决定肥皂膜形状的根本机制是建基于一条原则 - 尽可能达致最少物理能量(在理想情况下,大致就是曲面的面积)。这项听来简单的构念名为「最小作用量原理」(least action principle),可以用来在多种情况下衍生出许多物理定律,包括杨米理论(Yang-Mills theory)、爱因斯坦的广义相对论。虽然普拉托的实验为肥皂膜建立了一套完备的模型,但后来学者发现难以用严格的数学语言来证明该等肥皂膜曲面的存在。直至1930年,这项难题终于由Jesse Douglas及Tibor Radó各自分别解决,这是极重大的突破!这项成就之突出,使Douglas在1936年获颁第一个有「诺贝尔数学奖」之称的费尔兹奖章。约四十年后,Jean Taylor[3]发表《普拉托定律》的第一套数学证明,从而验证了普拉托在一个多世纪前从肥皂膜实验所得到的观察结果。
Jean Taylor在证明其著名理论时所用的技巧,与Douglas及Radó在解决普拉托问题时所用的不同。他的构思是属于数学里的一个研究领域,名为「几何测度论」(Geometric Measure Theory,GMT),在研究几何变分问题(geometric variational problems)所产生的物体(如肥皂膜及肥皂泡)之一般形状及精细结构方面,是极之有用的工具。
在一窥GMT所涉的内容之前,我们先仔细定义「曲面」为何物。在数学里,曲面是个看起来像小型弹性膜的二维空间。在一个曲面里,如果每个点都有明确的「切平面」(tangent plane)(换言之无任何利边或角),这个曲面就可算是「平滑」。 GMT的一项重要技巧是爆发过程(blow-up process)。简单而言,如果想要了解曲面某个点周围的精细局部结构,可以假想用显微镜放大该点周围的区域。当不断增加显微镜的放大率时,曲面的某个平滑点看起来就会越来越像平面。相反,如果将一个奇点(singular point)放大(例如肥皂膜的边缘或顶点),就会看到一些与平面不同的极限几何形状。透过研究从这些爆发过程可以得到的极限形状,我们可以推断出奇点周围的局部结构(图5)。这项构思远远超过极小曲面的范畴,但对研究晶界运动(grain boundary motion)[4]及融冰介面[5]中出现的奇点至关重要。
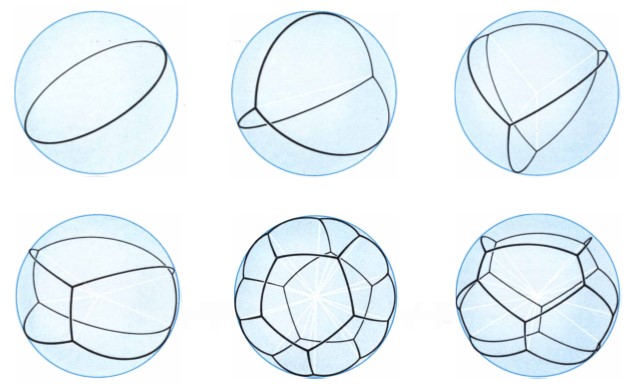
图5 - 在爆发过程中可能出现的一些极限几何形状(资料来源:“The Geometry of Soap Films and Soap Bubbles”《肥皂膜及肥皂泡的几何学》, F Almgren and J Taylor, Scientific American (1976))
有关极小曲面的一个自由边界问题 普拉托的问题属于数学家所谓「Dirichlet边界值问题」里的一般类型问题。为了令读者更加更有亲切感,我们会举出一个日常生活的例子。如果我们将空气吹入一杯牛奶内,会看到表面有一堆气泡形成,其中一部分黏在杯边(图6)。肥皂泡的边界可以在容器的内壁上自由移动(此处是玻璃),因此边界不是完全被固定的。 H A Schwarz在1872年观察到,肥皂泡(或肥皂膜)会与容器内壁垂直接触。这就是所谓的「自由边界问题」。

图6 - 黏在杯边的气泡(资料来源:https://www.masterfile.com/search/en/glass+of+milk+bubbles)
1816年,法国数学家Gergonne提出第一个有关极小曲面与自由边界的几何问题,但直到二十世纪三十年代,才由Richard Courant与他的学生对总体问题提出有系统的研究[6]。在任意形状的容器里,能否找出至少一个带有自由边界的极小曲面?这个问题虽然在过去几十年中取得了重大进展,但直至最近才得到概括而肯定的解决[7]。我们借鉴F Almgren与他学生J Pitts[8]在三十年前提出的理论,名为「极小极大理论」,它的作用是在非常普通的情况下透过几何测度论来构造极小曲面。 Almgren与Pitts的极小极大理论最近再次掀起话题,因为学者出奇地发现到它与共形几何(conformal geometry)[9]及纽结理论(knot theory)[10]中其他长期未被解决的问题有所关联。更令人意想不到的是,极小极大理论会产生不止一个,而是无限个极小曲面 [11](通常均匀分布在环绕空间(ambient space) [12] 内。
数学与物理学上的极小曲面 虽然极小曲面在我们熟悉的平面三维空间会更简单、更直观,但极小曲面的概念并不止于此。极小曲面亦存在于弯曲及更高维的空间。古典微分几何学里广为人知的一点是,环绕空间的曲率会影响「直线」的性质(图7)。我们可将极小曲面类比为「直线」的更高维版本;利用极小曲面这块透镜,我们就可以研究到周围空间的几何形状。 R Schoen与丘成桐运用极小曲面理论来证明广义相对论 [13] 中的正质量猜想(positive mass conjecture)。极小曲面在几何流(geometric flow)中自然出现,令几何拓扑学中有百年历史的「庞加莱猜想」(Poincare Conjecture) 得到证明[14]。单位球(unit ball)的自由边界极小曲面与形状最佳化问题息息相关[15]。最近的研究显示,黑洞的熵与AdS/CFT对偶(AdS/CFT correspondence)中出现的某些极小曲面的面积有关[16]。我们预计,极小曲面会在数学及物理学的诸多问题中担当重要位置,因为只需看看周围的环境,就会发觉到,极小曲面无处不在!
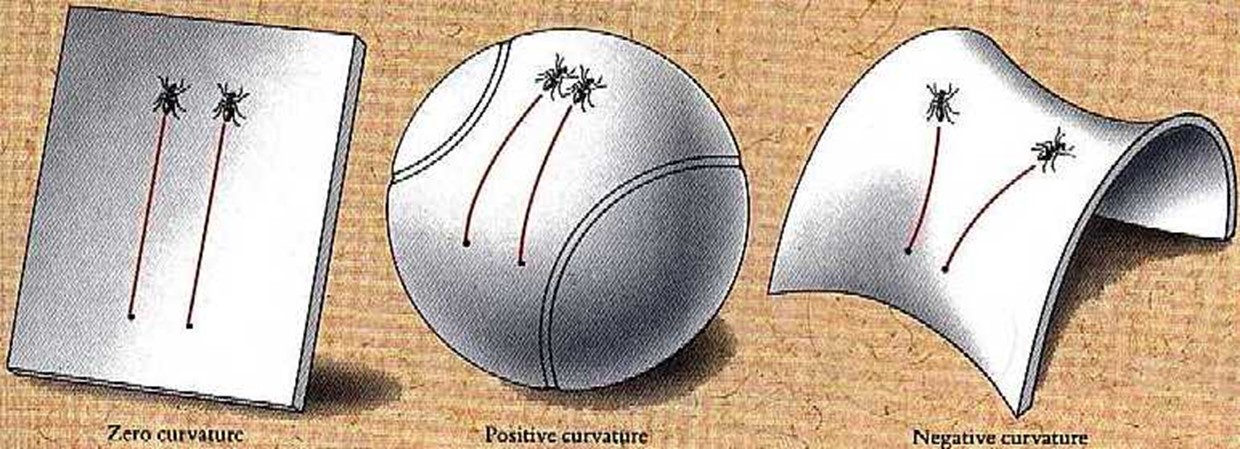
图7 - 几何形状影响直线的特性。平面上的两条平行线之间保持固定距离(左),而像网球的正弯曲空间里,直线会有汇合的倾向(中);在像马鞍的负弯曲空间里则会散开(资料来源:http://gemma.ujf.cas.cz/~krejcirik/images/ants.jpg)
References
- O. Savin, “Phase Transitions, Minimal Surfaces and A Conjecture of De Giorgi”, Current Developments in Mathematics, 2010: 59-113 (2010)
- B. Winter et. al. “Coexistence of both gyroid chiralities in individual butterfly wing scales of Callophrys rubi” PNAS 112 (42), 12911-12916 (2015)
- J. Taylor, “The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces”, Annals of Mathematics 103 (1976), 489-539
- K. Brakke, “The motion of a surface by its mean curvature”, Mathematical Notes, vol. 20. Princeton University Press, Princeton (1978)
- A. Figalli, X. Ros-Oton, J. Serra, “The singular set in the Stefan problem”, arXiv:2103.13379
- R. Courant, “Dirichlet principle, conformal mapping, and minimal surfaces”, Dover Publications (2005)
- M. M.-c. Li, X. Zhou, “Min-max theory for free boundary minimal hypersurfaces I: regularity theory”, Journal of Differential Geometry 118 (2021), no. 3, 487-553
- J. Pitts, “Existence and regularity of minimal surfaces on Riemannian manifolds”, Mathematical Notes, vol. 27, Princeton University Press, Princeton (1981)
- F.C. Marques, A. Neves, “Min-max theory and the Willmore Conjecture”, Annals of Mathematics 179 (2014), 683-782
- F.C. Marques, A. Neves, “Min-max theory and the energy of links”, Journal of the American Mathematical Society 29 (2016), 561-578
- A. Song, “Existence of infinitely many minimal hypersurfaces in closed manifolds”, arXiv: 1806.08816
- F.C. Marques, A. Neves, A. Song, “Equidistribution of minimal hypersurfaces for generic metrics”, Inventiones Mathematicae 216 (2019), 421-443
- R. Schoen, S.-T. Yau, “On the proof of the positive mass conjecture in general relativity”, Communications in Mathematical Physics 65 (1979), 45-76
- T. Colding, W. Minicozzi, “Width and finite extinction time of Ricci flow”, Geometry & Topology 12 (2008), 2537-2586
- A. Fraser, R. Schoen, “Sharp eigenvalue bounds and minimal surfaces in the ball”, Inventiones Mathematicae 203 (2016), 823-890
- S. Ryu, R. Takayanagi, “Aspects of Holographic Entanglement Entropy”, Journal of High Energy Physics 2006 (8): 045
作者︰
香港中文大学数学系副教授李文俊教授
2021年11月

