Big Bang and the Expanding Universe

One of the greatest scientific discoveries is the expansion of the universe. This expansion, along with the mutual gravity of matter, drives the universe's evolution, transforming it from a hot and uniform state to the cold and clustered phase we observe today. It is a cornerstone of modern cosmology and makes the Big Bang theory a household name. The current expansion rate, known as the Hubble constant, named after Edwin Hubble, who discovered it in 1929 by observing the apparent motions of nearby galaxies [1], is of fundamental importance in modern cosmology.

Many people mistakenly think that the universe's expansion is the result of a massive explosion—the Big Bang—that caused matter to fly apart from a fixed point in space, as shown in Fig 1. In this view, the explosion occurs at a unique location within otherwise empty space, which implies that we would need to be relatively close to this explosion point—the centre of the universe—to observe that most galaxies are moving "outward," as indicated by the Doppler redshift of their light, like the decreasing frequency of an ambulance's siren as it moves away from us.

Fig 1 Common mistaken view of the Big Bang: a giant explosion occurred, and matter flew apart from the centre into empty space. Light from galaxies suffers Doppler redshift as observed by us, who happen to live near the explosion centre.

However, such an explosion scenario contradicts the Cosmological Principle, a fundamental assumption of modern cosmological theories. This principle states that the universe is homogeneous and isotropic on large scales. In other words, we assume that the universe appears the same from any location and in every direction. If this assumption were not true, we would have no justification for believing that our observations from Earth provide an accurate representation of the universe. Furthermore, the concept of matter dispersing in a fixed, empty space contradicts General Relativity, which states that space-time and matter interact with each other. Even Einstein was astonished to discover that a static space is not a stable solution in General Relativity [2].

A view that aligns with both General Relativity and the Cosmological Principle is that space expands uniformly among galaxies (see Fig 2). From the perspective of any given galaxies, all other galaxies appear to be moving away in all directions. Moreover, the apparent speed at which a galaxy is receding is proportional to its distance from the observer.

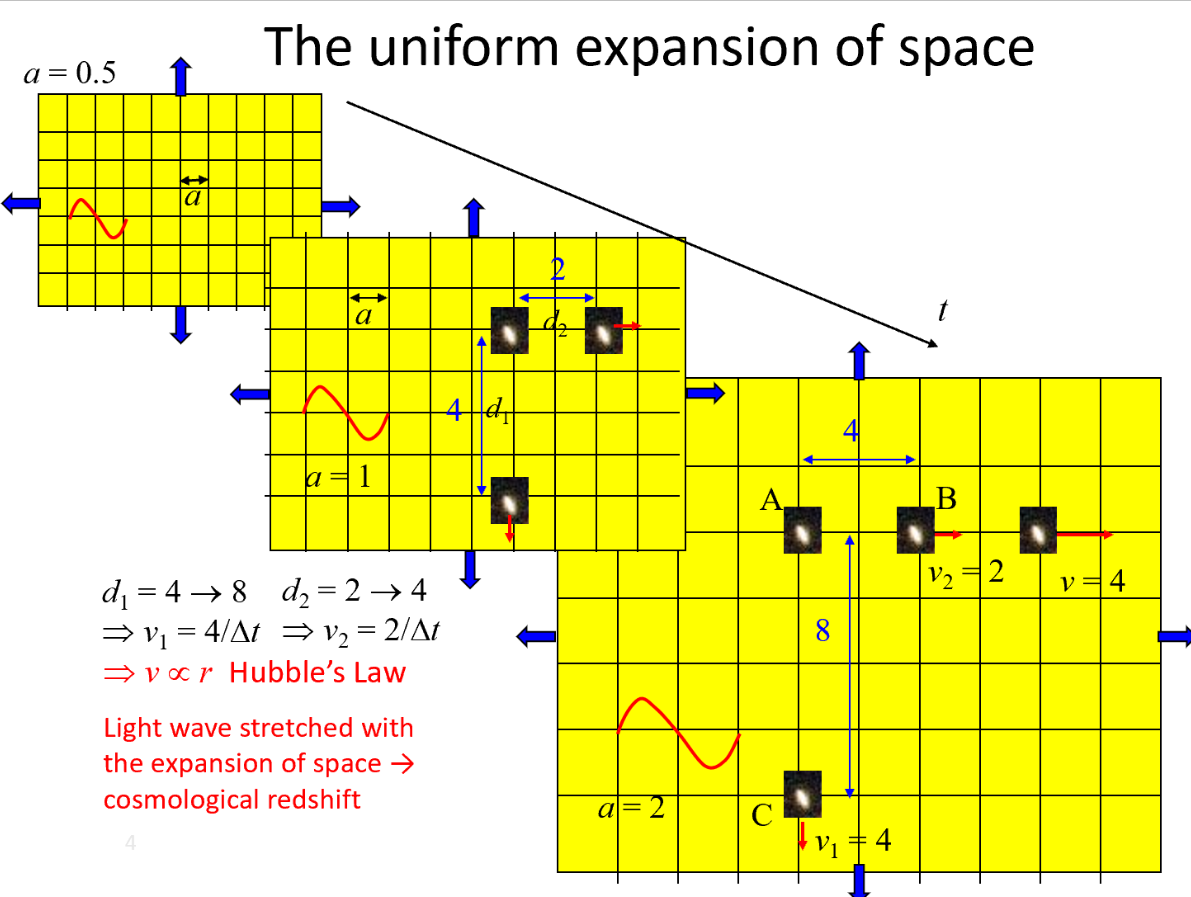
Fig 2 The universe's expansion should be understood as the uniform expansion of empty space between distant galaxies. A uniform grid can be drawn to illustrate the relative sizes of this space, which is measured by the cosmological scale factor, denoted as a, and it increases over time. Hubble's Law describes this uniform expansion of space. This understanding aligns with both the Cosmological Principle and General Relativity.

For example, let's consider galaxies B and C, which are located at distances of 2 and 4 units from galaxy A, respectively, at time t = t₀. By time t = t₀ +∆t, the distances to galaxies B and C are both doubled due to the uniform expansion of space. Thus, their distances from A increase to 4 and 8 units, respectively. As a result, from A's viewpoint, galaxies B and C appear to recede at speeds of 2/∆t and 4/∆t units, respectively, demonstrating a perfect proportional relationship to their distances. We have concluded that v = Hd, where H is the proportionality constant known as the Hubble parameter. This relationship is known as Hubble's Law. In this model, every point in the universe is considered a centre of expansion, with grids extending infinitely in all directions, ensuring that the universe remains homogeneous and isotropic.

Due to the universe's expansion, the density of matter and energy decreases over time. As a result, the universe evolves from an initially hot and dense state into the cold and diffuse condition we observe today. The Hubble parameter, H, also changes with time. Cosmological models, such as the Ʌ (for dark energy) Cold Dark Matter (ɅCDM) model [3], predict how H varies and describe the universe's expansion history (see Fig 3), which can be tested against observation. In particular, the current expansion rate, known as the Hubble constant H₀, has been widely measured using various methods [4].

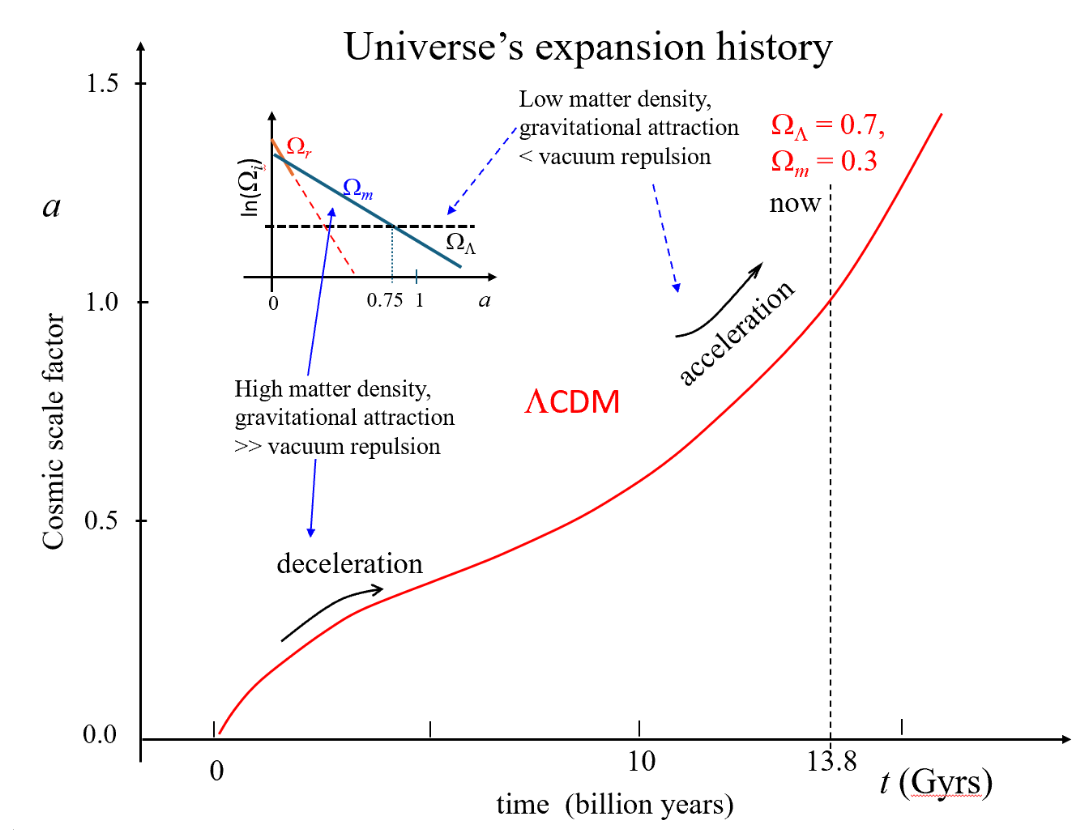
Fig 3 A sketch of the universe's expansion history according to CDM. The decelerating early expansion transitions to the late acceleration due to the weakening mutual gravitational attraction as matter density drops.

The Hubble Tension – Cosmology in Crisis

Recently, a significant discrepancy has emerged in the measured values of the Hubble constant [5]. These measurements can be divided into two categories: local measurements based on light from relatively nearby objects, such as supernovae, and global measurements derived from observation of the cosmic microwave background, assuming the standard cosmological model. While local measurements report values around 73 ± 1 km/s/Mpc, meaning that two galaxies separated by 1 Mpc (about 3.3 million light-years) appear to recede from each other at the speed of 73 km per second, global measurements prefer 67 ± 0.5 km/s/Mpc.

Local measurements directly determine the Hubble constant using Hubble's Law, H₀ = v/d. While the line-of-sight speed of a nearby object v can be measured through the redshift of its light, determining its distance d is more challenging. Fortunately, the intrinsic brightness of some cosmic objects is known or can be measured easily. These are called standard candles. For example, Cepheids are variable stars that follow a tight correlation between their brightness variation period and intrinsic brightness, and the former is relatively easy to measure. Once an object's intrinsic brightness is known, the comparison to its apparent brightness tells us its distance since the latter falls off as distance squared. Astronomers use nearby standard candles, such as Cepheids, whose distances can be measured by multiple methods to cross-check and are therefore more reliable, to calibrate standard candles that are farther away, such as Type 1A supernovae [6].

Such local measurements do not rely on a particular cosmological model. However, systematic errors may arise with the distance measurements, particularly since whether a 'standard candle' is really 'standard' may be debatable.

Furthermore, the measured redshift of an object may not be entirely due to the Hubble expansion and therefore not completely correspond to H₀d. Any cosmic object can be attracted by its neighbours, leading to deviations in its motion from the Hubble expansion (see Fig 4). This phenomenon is known as peculiar motion. In other words, referring to Fig 2, we should not assume the galaxies to remain stuck on the grids. They also move relative to the grids, due to their interaction with nearby objects. A galaxy's peculiar motion contributes to its line-of-sight velocity in addition to the Hubble expansion, v = vp + H₀d. While H₀d is always positive, vp can be positive or negative.

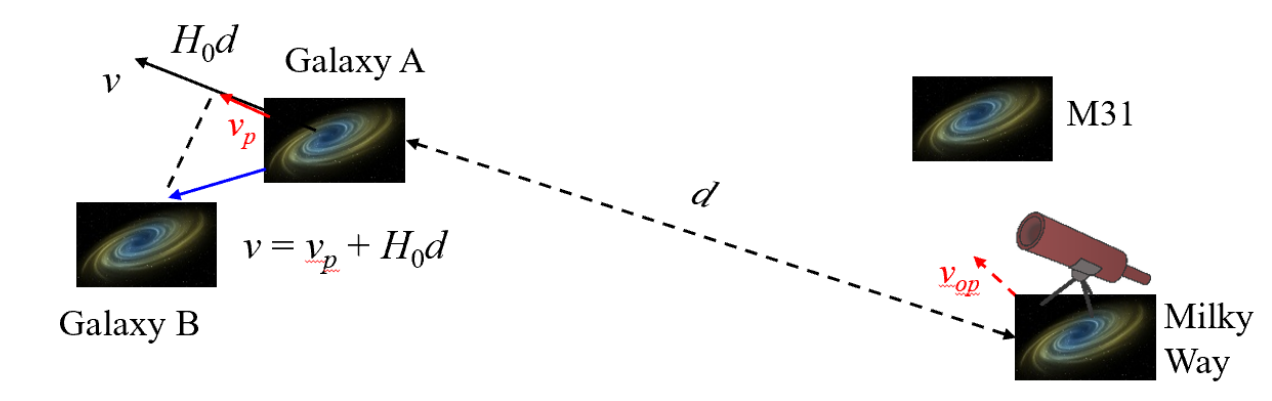
Fig 4 Peculiar motion of Galaxy A due to its interaction with Galaxy B would cause an additional contribution to the speed observed by us, vp. Milky Way's peculiar motion, such as due to attraction by our neighbour M31, indicated by the red dashed arrow, also affects local measurements of H₀.

According to the Cosmological Principle, the peculiar motions of cosmic objects should vary in random directions and magnitudes, so when averaged over many objects, their contributions to H₀ should effectively cancel each other out. However, our observations are also affected by our peculiar motion relative to the Hubble expansion, which would not be cancelled out by averaging over many measurements, resulting in a systematic error in the measured value of H₀.

Global measurements of the Hubble constant (H₀) depend on standard length scales derived from the acoustic waves in the early universe's hot plasma. This plasma was opaque to photons for about 400,000 years, during which the universe was hotter than approximately 3000 K. As the universe expanded and cooled below this temperature, the plasma transitioned to neutral hydrogen gas, similar to how water vapor condenses into liquid at 100 °C. Once this transition occurred, photons emitted from the plasma could travel freely through the neutral gas, the so-called photon decoupling.

These photons still exist today, but their wavelengths have been stretched with the cosmic expansion by about 1100 times to form the Cosmic Microwave Background (CMB) [7]. The full-sky CMB temperature distribution has been measured precisely by missions such as WMAP and Planck, providing a snapshot of the CMB sky at photon decoupling (see Fig 5). The seemingly random pattern of temperature fluctuations in the CMB is created by the interference of many acoustic waves that were excited in the primordial plasma. Detailed analyses of these fluctuations provide a wealth of information about the universe, including important cosmological parameters [8].

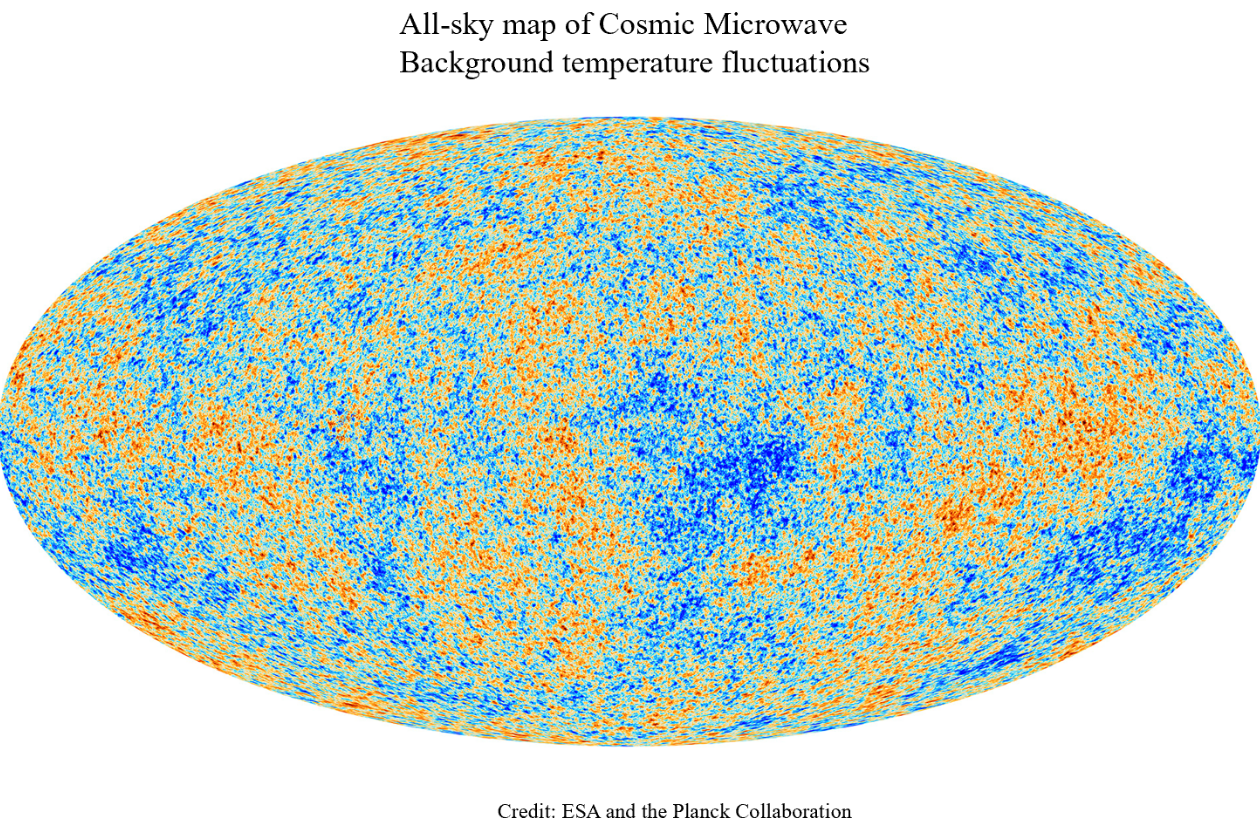
Fig 5 Snapshot of the full-sky CMB temperature distribution when the universe was about 380,000 years old. The colours indicate slightly hotter (red) to colder (blue), by about 10⁻⁴ K around a mean temperature of 2.725 K. Credit: ESA/Planck Collaboration.

The fundamental mode of acoustic oscillations, which is akin to the simplest standing wave created by a string fixed at both ends, establishes an angular scale, θ , of approximately 1° on the CMB map (see Fig 6). At this scale, the temperature fluctuations are significantly correlated. The baseline of this θ angle is the distance of the photon decoupling surface to us, D, which depends on the expansion history of the universe since photon decoupling and therefore is sensitive to H₀. The value of H₀ is thus related to the angle θ. While θ can be measured to high precision by CMB observations, a model of the cosmological expansion history needs to be assumed to extract H₀. Therefore, global measurements of H₀ rely on the correctness of ɅCDM.

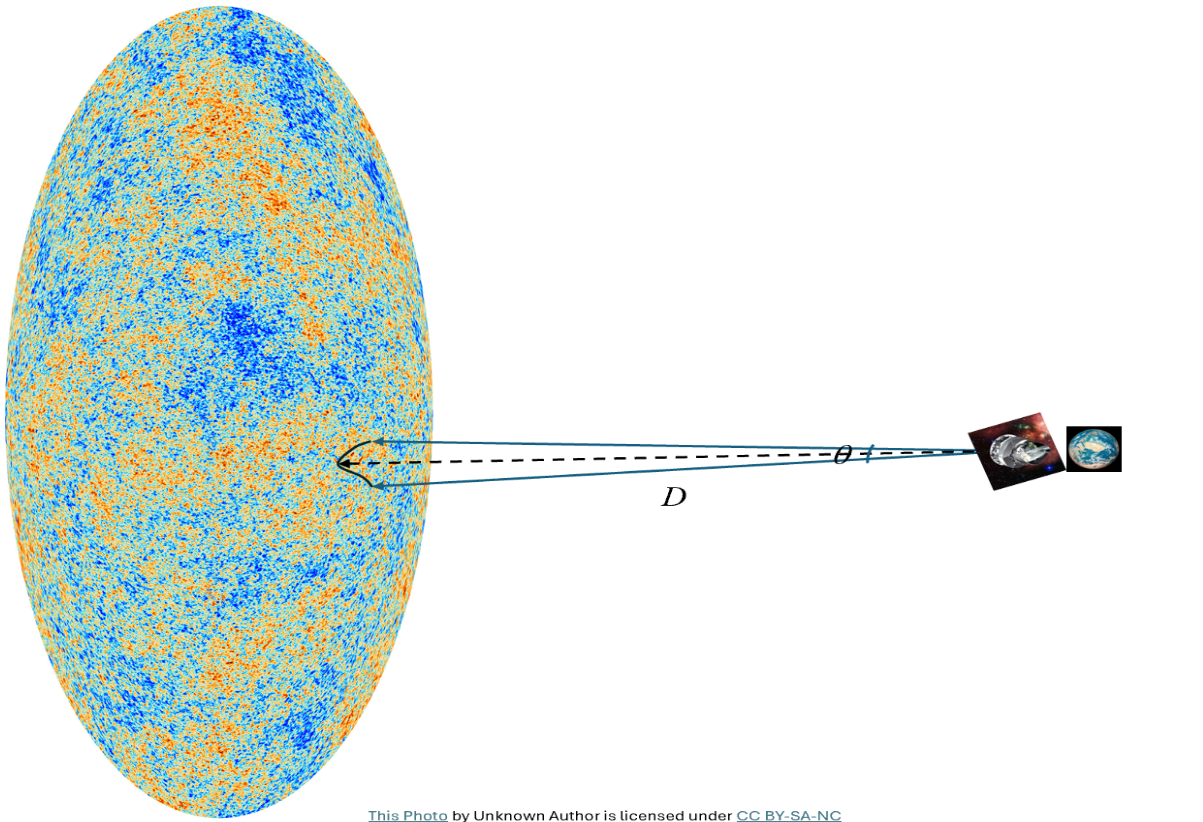
Fig 6 Measuring the correlation angle of CMB temperature fluctuations from Earth. The sound horizon at the photon decoupling surface subtends an angle θ over a distance D.

The issue known as the Hubble Tension has generated significant excitement and attention because it may suggest the existence of new physics that goes beyond the standard ɅCDM cosmological model and the Standard Model of Particle Physics. For example, one potential solution to the Hubble Tension is the introduction of previously undetected radiation, beyond just photons and neutrinos, referred to as dark radiation. This addition could alter the universe's expansion history compared to ɅCDM's and align the measurements of Hubble's constant (H₀) from the CMB with the values measured locally. The existence of such dark radiations, if confirmed, would represent an important breakthrough in fundamental physics.

Given the importance of the Hubble Tension, it is of high priority for researchers to find independent and reliable methods to measure H₀ to check both the local and global measurements.

Uncovering the hidden dynamics of galaxy pairs

A recent study conducted by our team from the Department of Physics at The Chinese University of Hong Kong introduces a new method for measuring the Hubble constant [9]. The team includes PhD student Wangzheng Zhang, Dr Shek Yeung, a CUHK PhD graduate from 2022, along with collaborators Dr Shihong Liao, who received his PhD from CUHK in 2015 and is affiliated with the National Astronomical Observatories of China, and Dr Hui-Jie Hu from University of the Chinese Academy of Sciences. Our findings, published in the Astrophysical Journal Letters, detail a novel approach that analyses the mutual motions of galaxy pairs to measure H₀.

Instead of measuring H₀ by observing the apparent motion of individual galaxies, we focused on the relative motions of pairs of galaxies. These motions are affected by both their mutual gravitational interactions and the Hubble expansion of the universe. We utilised a statistical measure known as pairwise velocity, which describes the relative motion between galaxy pairs and provides valuable insights into the structure and evolution of the universe. By examining this motion, we could infer key details about the large-scale dynamics of the universe, including the Hubble constant.

We used advanced computer simulations, called cosmological N-body simulations, to model pairwise velocities across different expansion scenarios. We compared the results of these simulations with observational data collected from galaxy surveys. Our findings indicated that pairwise velocity could be used as an independent and accurate measurement of H₀, offering a new perspective on the Hubble Tension.

A New, More Reliable Approach to Measuring the Hubble Constant

This new method focuses on the relative velocity between galaxies within pairs, effectively minimising common biases, including those introduced by our peculiar motion relative to the Hubble expansion. As illustrated in Fig 7, the observed velocities of Galaxies A and B,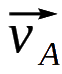 and , respectively, both include the same contributions from the observer's peculiar motion (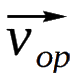), but they are exactly cancelled in the relative velocity between Galaxies A and B, 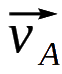- . Similarly, other systematic errors common to the measurements of 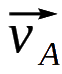and , such as due to the observer's instrument, also largely cancel in the pairwise relative velocity. As a result, this approach is more reliable and complements existing methods for measuring the Hubble constant.

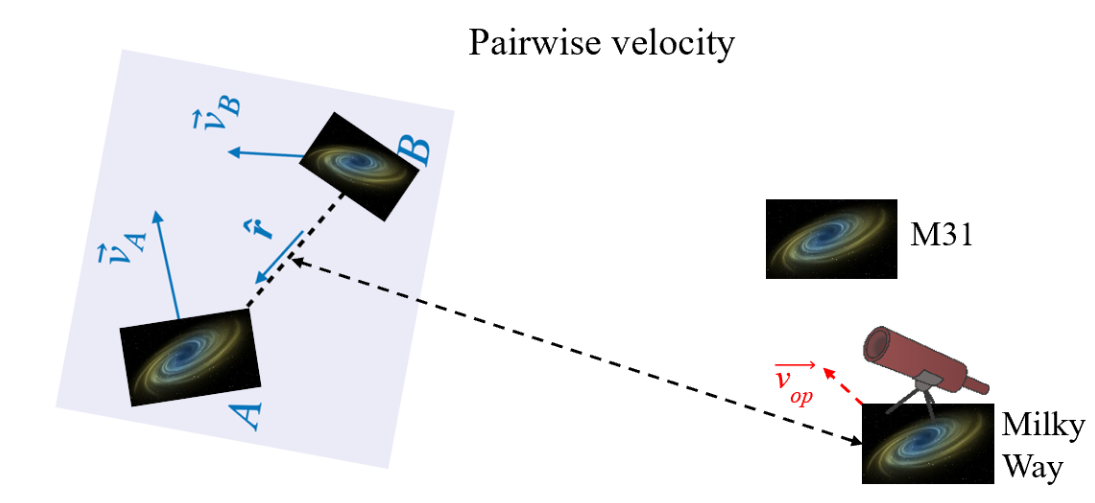
Fig 7 Pairwise velocity is defined as the relative velocity between two galaxies, such as Galaxies A and B, projected along their line of separation, shown as the dashed line. Since the observed velocities of Galaxies A and B, 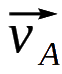and , respectively, include the same contributions from the observer's peculiar motion, they cancel out in the relative velocity.

The new measurement places the Hubble constant at 75.5 km/s/Mpc, with an uncertainty of 1.4 km/s/Mpc, about 2%. This result is consistent with other local measurements. This has reaffirmed the Hubble Tension with greater significance, further challenging the standard cosmological model.

Furthermore, as the motions of galaxies are also affected by their mutual gravitational interactions, the pairwise velocity averaged over many galaxies is sensitive not only to H₀, but also to the mean matter density of the universe. Using the new method, we obtained an independent measurement of the cosmological parameter Ωₘ, representing the fractional contribution of matter in the total energy density of the universe. Our measurement yields ❲Ωₘ❳ = 0.311 with an uncertainty of less than 0.03, or 9%. This result agrees well with the value provided by the Planck Collaboration, which is based on observations of CMB and other cosmological data [8].

With the upcoming large-scale surveys, such as the LSST [10], many more cosmic objects will be measured with greater precision. While our method is currently limited by statistical errors, these will be significantly reduced in the future. We estimate that using our method, the uncertainties of H₀ and Ωₘ can be reduced to 0.6% and 2%, respectively.

The pairwise velocity is a valuable tool in cosmology. Not only does it help us measure the Hubble constant H₀ and matter density Ωₘ, but it also allows us to investigate the effects of cosmological neutrinos and other hypothetical light dark matter particles. These light cosmic particles move much faster than cold dark matter, which enables them to smooth out the large-scale structures formed by cold dark matter. This, in turn, affects the gravitational interactions among matter, and we can observe these changes through pairwise velocity measurements.

By conducting cosmological N-body simulations, both with and without these light particles, we can compare their effects on pairwise velocity. This method provides valuable insights into the properties of cosmological neutrinos [11] and helps us place constraints on the existence of light sterile neutrinos [12]—hypothetical particles that are even more inert than familiar neutrinos [13]. We are also working on employing the method to determine the neutrino mass, which is so small that even the best laboratory experiments today cannot directly measure it.

That is the beauty of Cosmology. The universe conducts the largest experiment for us to observe, and even the tiniest particles, like the neutrinos, leave their marks. With larger and more advanced telescopes, we can observe more of the universe's history, almost all the way back to the Big Bang.

We are truly fortunate and privileged to contribute, no matter how small, to this great quest for understanding the evolution of the universe.

References:

1. E. Hubble, “A relation between distance and radial velocity among extra-galactic nebulae”. Proceedings of the National Academy of Sciences, 15, 168 (1929).
2. See for example, S. Weinberg, “Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity” (Wiley, 1972).
3. See for example, https://lambda.gsfc.nasa.gov/education/graphic_history/univ_evol.html; https://ned.ipac.caltech.edu/level5/Peebles1/Peeb2.html
4. For recent reviews, see R. B. Tully, “The Hubble Constant: A Historical Review,” https://arxiv.org/abs/2305.11950 ; W. L. Freedman, B. F. Madore, “Progress in Direct Measurements of the Hubble Constant,” https://arxiv.org/abs/2309.05618.
5. For a recent review, see E. D. Valentino et al., “The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics,” https://doi.org/10.48550/arXiv.2504.01669
6. A. G. Riess et al., Astrophysical Journal Letters, 934, L7 (2022) and references therein.
7. An excellent review of CMB physics can be found in https://background.uchicago.edu/~whu/araa/node1.html.
8. Planck Collaboration, “Planck 2018 results. I. Overview and the cosmological legacy of Planck,” Astronomy & Astrophysics, 641, A1 (2020).
9. W. Zhang et al., “Measuring the Hubble Constant through the Galaxy Pairwise Peculiar Velocity,” Astrophysical Journal Letters , 978, L6 (2025).
10. Legacy Survey of Space and Time https://rubinobservatory.org/for-scientists/rubin-101
11. W. Zhang et al., “Measuring neutrino mass and asymmetry with matter pairwise velocities,” Monthly Notices of the Royal Astronomical Society, 529, 360 (2024).
12. R. Hu et al., “Impact of light sterile neutrinos on cosmological large scale structure,” https://arxiv.org/abs/2501.16908.
13. B. Dasgupta and J. Kopp, “Sterile Neutrinos”, Physics Reports ,928, 1 (2021).



Author:
Prof Chu Ming Chung, Department of Physics, The Chinese University of Hong Kong

June 2025